Bayesian Classifier

Introduction

Salmon – Sea Bass Problem : 연어-논어 분류 문제

• 연어와 농어로 분류하는 것을 원함
• 우리는 카메라를 통해 특성을 추출하는 것을 원한다 (길이, 밝기, 넓이 등등)

밝기와 넓이로 분류해보면

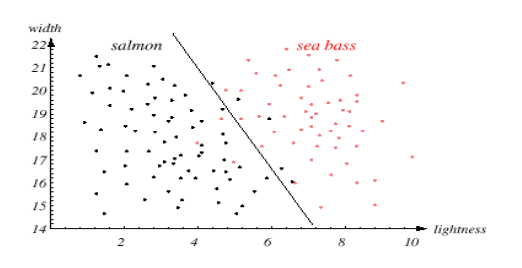
이차원 Data Model

위의 선은 dexidion boundary (class boundary, decision hyper-plane 초평면)

Bayesian Classifier

우리는 데이터를 몇개의 class로 분류하고 싶다.

우리가 알기를 원하는 것은 임의의 data x가 들어왔을때 j번쨰 클래스에 속할 확률을 구하고 싶다.

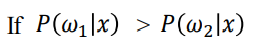
이라면 데이터 x는 class 1이라고 결정한다.

Bayes’ formula

classification 확률에 Bayes’ formula를 적용할 수 있다.

총 네개의 parameter을 확일할 수 있다.

Posterior, likelihood, prior, evidence

Prior

사전 확률

데이터와는 상관 없는 값, 자연상에 존재하는 확률

Prior 확률은 수집한 traning data와는 독립적이다.

Likelihood

현재 수집된 data의 빈도수 <= data에 의존적이다.

지금 얻은 데이터가 이 분포로부터 나왔을 가능도를 의미한다.

• class-conditional probability 라고도 부른다.
• 데이터가 기여되는 부분이다.

따라서 data기반, 통계 기반 이라는 말은 likelihood를 이용해 판단한다는 말과 비슷함

Evidence

Marginal probability of x to wj : wj의 x의 한계확률

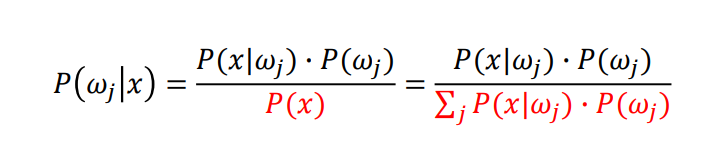
위처럼 j의 영향력을 없애버릴수 있다.

evidence는 j에 독립적이다.

• 따라서 decision boundary에 영향을 미치지 않는다. (scale factor => 확률분포로 나오게 하기 위한 요소)

• posterior의 probability disribution을 만들기 위하여 사용한다.

(Normal * Normal = Normal)

Posterior

사후확률

classifiacion의 확률

• prior(사전확률)과 likelihood(우도)에 기초한 decision boundary를 결정한다

• decision = likelihood * prior

  (decision = Observed data _ Prior knowledge = 현재 데이터 _ 과거의 사전 지식)

Parameter Estimation

파라미터 추청

Generative vs Discriminative

Generative 생성모델

• 모델링의 결과로 부터 data를 생성하는 것이 목표
• ex) GAN

Discriminative 판별모델

• 판별식(Discriminant function)을 찾는 것이 주 목적

Parametric vs. Non-parametric

Parametric : 모델에서 미리 정의된 파라미터들을 찾고, 최적화 하는것

Non-Parametric : 모델에 파라미터가 없음

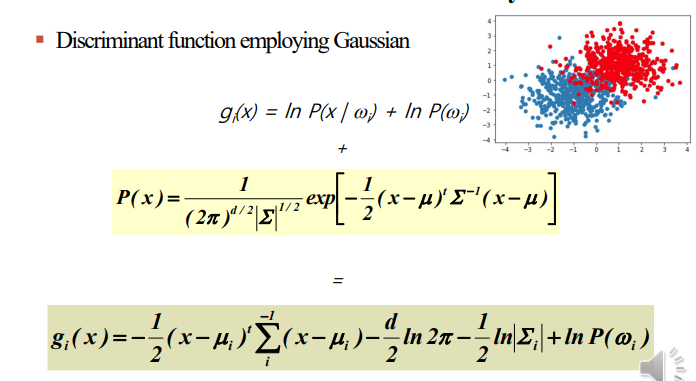
Discriminant Function for Decision Boundary

각각의 클래스에서

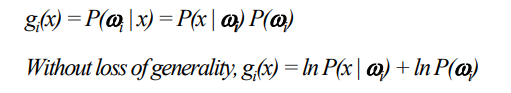
log는 단조증가이므로 커지기만 할뿐 순서가 바뀌지 않는 함수이다.

따라서 log를 씌워도 나중에 판별할때 차이가 없으며, 일관성을 읽지 않는다.

따라서 Decision boundary는 밑과 같이 결정할수 있다.

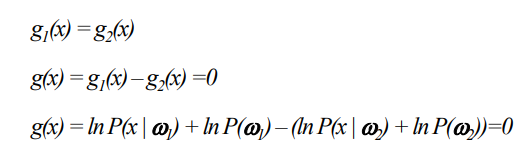
가우시안 분포 (Gaussian distribution)

가장 일반적으로 사용할 수 있는 분포

• 관찰된 데이터에서 추정된 확률함수는 class-conditional이다.

• 우리는 class-conditional 이 가우시안 분포를 따른다고 가정한다.

Univariate and multivariate Gaussian

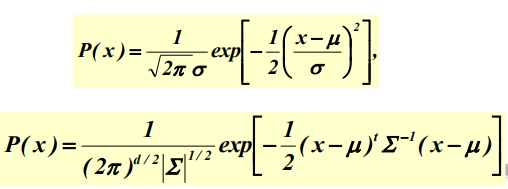
x : random value

=> 평균과 표준편차 값을 알면 정규분포식을 찾아낼 수 있다.

가우시안의 parameter를 어떻게 알수있을까?

이 두가지만 알면 된다.

Maximum Likelihood Estimation (MLE)

당연히 training data에 근거해야 한다.

• 확률 함수를 최대화 하는 parameter을 데이터를 가지고 추정하자 = Maximum likelihood

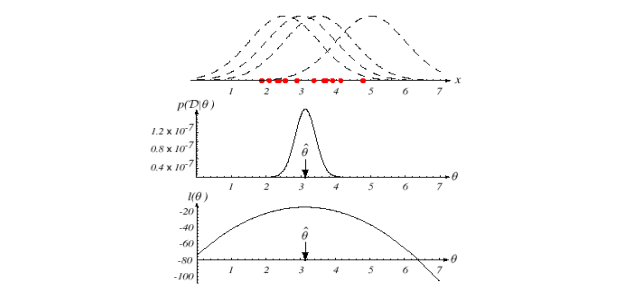
이런 식으로 최대값을 구하자. θ가 parameter

Generative and parametric approach

• parameter은 고정된 것으로 추정하였지만, 없는값이다.
• 최고의 parameter은 관찰된 것에 기초한 확률을 최대화하여 얻는다.
• 샘플의 크기가 증가하면, 추정은 좋은 covergence를 얻을수 있다.

즉, 가능도는 각 데이터 샘플에서 후보 분포 P(θ)P(θ)에 대한 y value(밀도)를 (데이터의 추출이 독립적이고 연달아 일어나는 사건이므로) 곱하여 계산한다.

직관적으로 생각했을 때 후보가 되는 분포가 데이터를 잘 설명한다면 likelihood는 당연히 높게 나올 것이다.

ML은 θ를 추정한다. maximizeds P(D

θ)를 찾기 위하여!

log-likelihood

=> 계산을 쉽게 하기위해서 사용

• log-likelihood는 일때 최대가 된다.

case 1 :

분산은 아는 경우

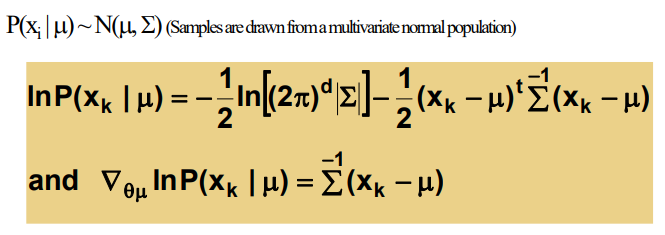
=> 1~k 까지 더하면 likelihood가 됨

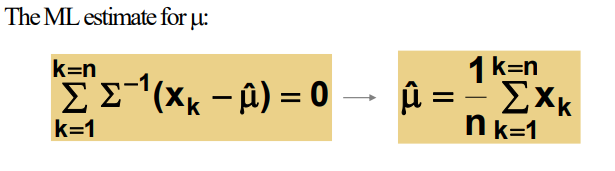
결론 : μ = data들의 산술 평균

case 2 :

둘다 모르는 경우

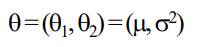=> θ로 표현해놓고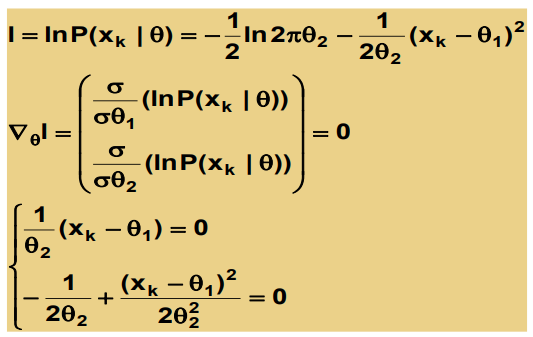

미분한 값이 0이 되는 부분이 최대가 되는 부분이므로 미분하여 0이되는 θ의 값을 찾는다.

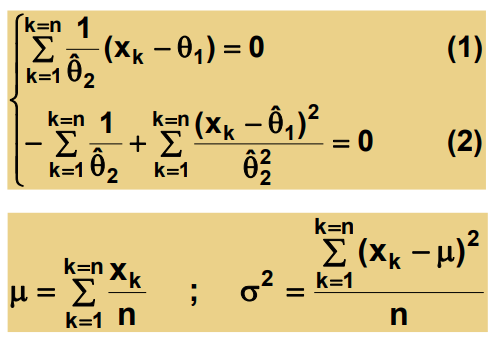
Bayesian Classifier

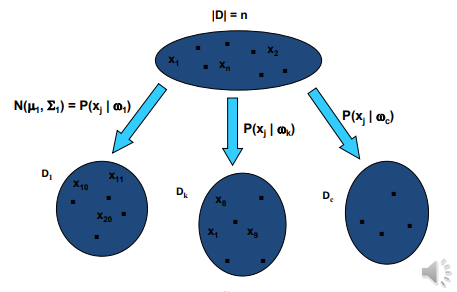
Naive Bayesian Classifier

높은 차원의 θ를 측정하려니까 힘들었다.

매우 복잡하고 많은 시간이 소요되었다.

그래서 Naive Baysian classifier은 매우 강력한 가정을 가진다.

• 모든 feature들은 독립적이다 -> 계산이ㅣ 간단해진다.

Problem definition

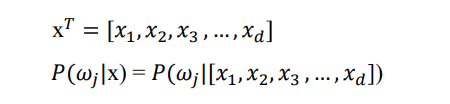
Bayesian 공식에서는

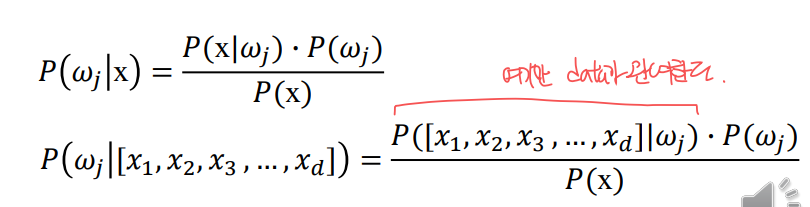
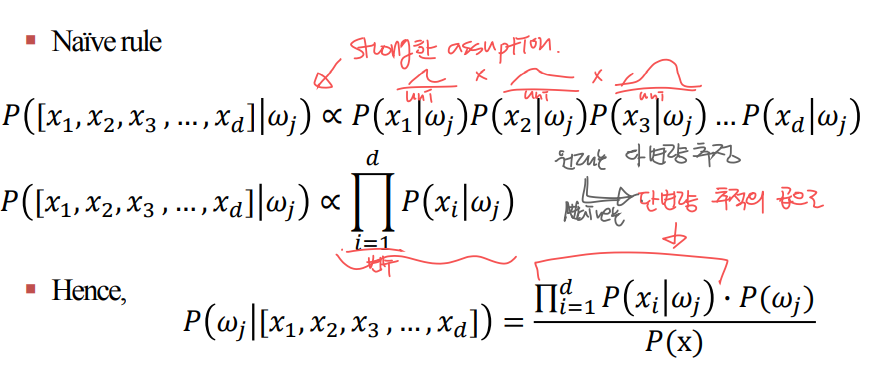
다차원 tack를 한 차원의 숫자로 줄인다.

• 다변량 분포 추정 -> 단변량 분포 추정

Bayesian Belief Network

직접적인 비순환 네트워크로 변수들의 real-world 관계를 표현

• node는 feature

  class를 의미한다.

• like는 conditional probability (relation)를 의미

Joint probability of p(a,b,c)

• p(a,b,c)=p(c

  a,b)p(a,b)

• p(a,b,c)=p(c

  a,b)p(b

  a)p(a)