Regression

Part 1. Linear Regression

Introduction

Sugpervied Learning

Regression Method

• Prediction method
• Supervised learning (y값 존재, target 존재)
• 예측할 y-value
  • 연속적인 값
  • ex)돈, 강수량

Regression Algorithms

Linear regression : 선형 회귀분석, y가 연속적이다. 관계가 linear

Multivariate linear regression : 다변량 선형 회귀분석

Lasso and Ridge linear regression : regularized (제약)

Neural network regression

Support vector regression

Decision tree regression

Linear Regression

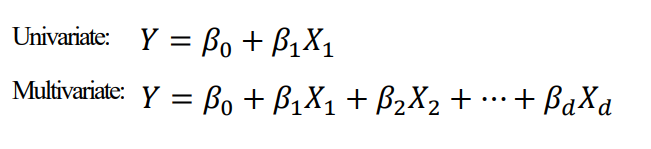
linear (선형)으로 모양을 정의

linear relationship은 선이나 hyperplane으로표현된다.

univariate linear regression 예시

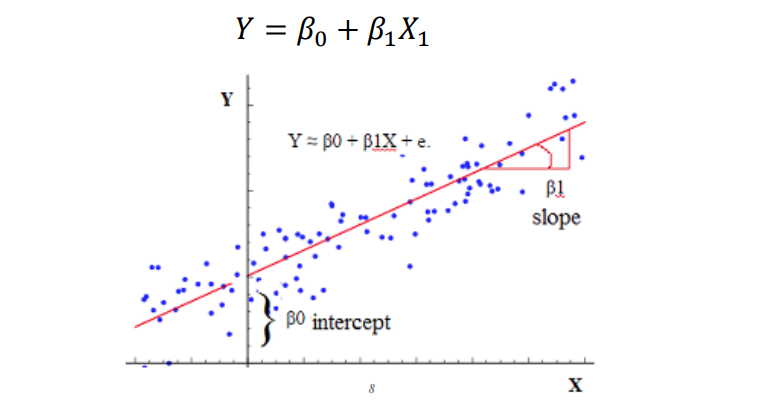
어떻게 β를 찾을까?

Least squres method

residual error 를 추정할 수 있다.

error = 실제값 - 예측 값

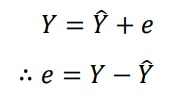
우리가 궁금한 것은 error의 총합이므로, 제곱을 해준다.

Residual Sum of Squares, RSS

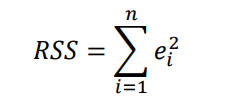
RSS의 최소를 찾아야 한다.

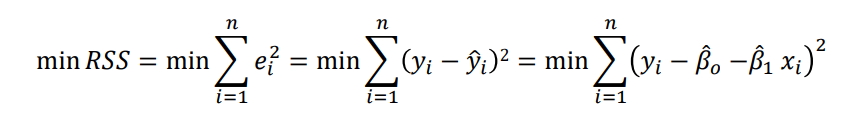
위에 따라서 explicit solution을 찾을 수 있다. => linear regression의 매우 중요한 장점 (단일해, 유일해)

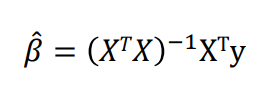
linear regression model은 높은 해석력을 가진다.

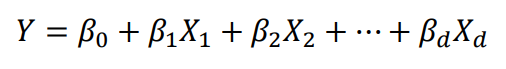
βi : Y의 변화량, Xi가 변화할 때

β0 : Y의 base line, Xi가 모두 0일때 (if zero-centered) <- x가 모두 0이라면 기본값 이라는 것 이기 때문에

장점

• 사용하기 쉽고, popular
• explain with prediction
• 변수 선택 방식이 발전하기 쉽다.

단점

• 오직 linear relationship만 찾을수 있다.
• 쓸데없는 features, 중복되는 features 발생
• fit, prediction이 좋지 않을 수 있다.

Part 2 . Evaluation and Regularization

Model Evaluation

Performance Measurements

성능 평가 지표 -> 정량적 평가

error = y - y_hat 기반

error의 총합은 모두 낮을수록 좋다.

• MSE = Mean Square error

  미분가능, 원래 scale을 쓴다.

  but, 큰 값에 너무 휘둘릴수 있다. -> RMSE

• RMSE = Root mean square error

• MAE